逻辑回归（Logistic Regression）虽然名字中包含“回归”，但它实际上是一种用于分类问题的统计方法。这种名称上的混淆可能源于逻辑回归与线性回归的相似性，以及它在处理二分类问题时使用的数学形式。

逻辑回归和线性回归的目标都是训练得到一条直线，不同的是，线性回归的直线尽可能去拟合输入变量X的分布，使得训练集中所有样本点到直线的距离尽可能短（图1）；而逻辑回归的直线尽可能去拟合决策边界，使得训练集样本中不同类的样本点尽可能分离开（图2）。

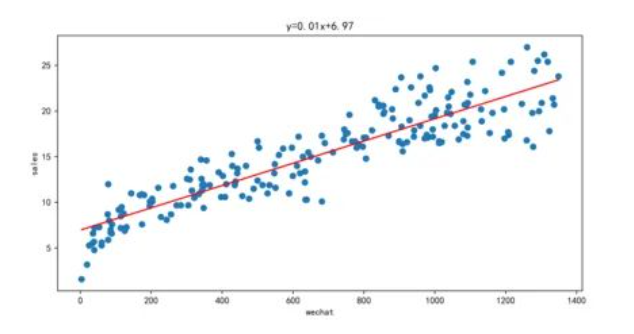
图1

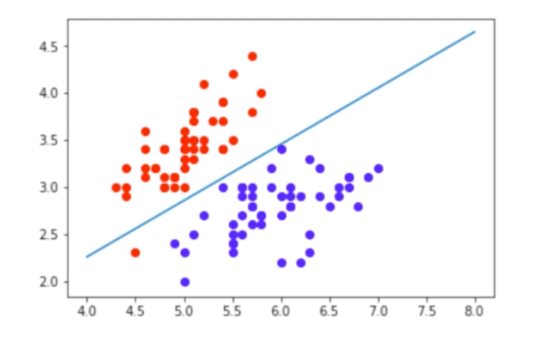
图2

可以简单理解为：如果预测值是连续的，就是回归问题；如果预测值是离散的，就是分类问题。为什么这么说呢？

逻辑回归的目的是预测一个样本属于某个类别的概率。它通过应用一个逻辑函数（也称为sigmoid函数）将线性回归的输出映射到0和1之间的概率值。sigmoid函数的定义如下：

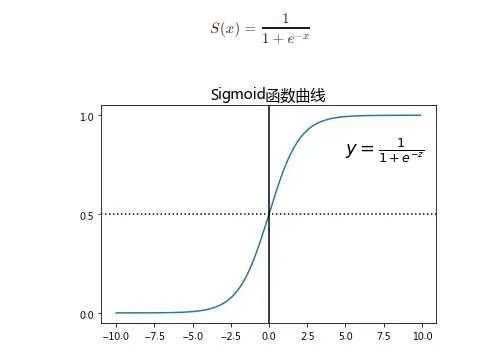
这个函数的输出始终位于0和1之间，非常适合描述概率。

逻辑回归模型通常用于二分类问题，其中输出只有两个可能值，例如“是”或“否”，“阳性”或“阴性”。模型的输出是一个概率值，表示样本属于正类（通常标记为1）的概率。我们可以设置一个阈值（通常为0.5），如果模型的输出概率大于这个阈值，我们就将样本分类为正类；否则，将其分类为负类（通常标记为0）。

逻辑回归模型的参数是通过最大化对数似然函数（也称为交叉熵损失函数）来估计的，这个函数衡量的是模型预测的概率分布与实际标签之间的差异。

通过一个例子来解释线性回归和逻辑回归。

线性回归例子：假设你想预测房屋的价格。收集了一些数据，包括房屋的大小（平方英尺）、卧室数量、浴室数量以及位置等信息。你的目标是建立一个模型，当你有新的房屋信息时，可以预测它的价格。

你可以使用线性回归来建立这个模型。线性回归会寻找一个最佳拟合平面（在二维空间中是一条直线），通过最小化所有数据点到这个平面的垂直距离的平方和来预测价格。模型的形式可能是：

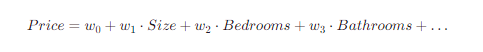
其中，w0,w1,w2,w3,… 是模型参数，通过最小二乘法或其他优化方法来确定。

逻辑回归例子：假设你想预测一个客户是否会购买房子。收集了一些客户的数据，包括他们的年收入、年龄、婚姻状况等信息。你的目标是建立一个模型，当有新的客户信息时，可以预测他们购买房子的概率。

你可以使用逻辑回归来建立这个模型。逻辑回归不会直接预测一个连续的价格，而是预测一个客户购买房子的概率。模型的形式可能是：

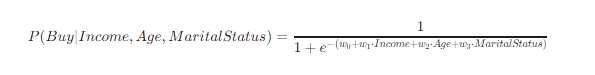
其中，P(Buy|Income,Age,MaritalStatus)是客户购买房子的条件概率，w0, w1, w2, w3 是模型参数，通过最大化对数似然函数来确定。

在这个例子中，逻辑回归的输出是一个介于0和1之间的概率值。你可以设置一个阈值（例如0.5），如果模型的输出概率大于这个阈值，就预测客户会购买房子；否则，预测他们不会购买。

总结来说，逻辑回归之所以属于分类问题，是因为它的目的是根据输入特征预测一个样本属于某个类别的概率，而不是预测一个连续的数值（如线性回归所做的）。逻辑回归的名称可能会让人误解其为回归方法，但实际上它是一种广泛应用于分类问题的统计学习方法。

看到这里，你是否觉得逻辑回归只可以处理二分类问题呢？

答案当然是否定的，既然可以处理二分类问题，那将多个二分类问题结合在一起，就可以处理多分类问题：

例如，想要预测一个水果是苹果、香蕉还是橙子，可以训练三个逻辑回归模型：

一个模型区分苹果和其他水果。

一个模型区分香蕉和其他水果。

一个模型区分橙子和其他水果。

然后，根据这三个模型的输出概率来决定这个水果最可能属于哪个类别。在预测时，哪个模型的预测概率最高，就将实例分到哪个类别。

虽然逻辑回归可以用于多分类问题，但在实践中，还有其他模型如支持向量机、决策树、随机森林等，并且可能更加有效。