信号处理的宗旨是“将信号中蕴涵的信息变得显然”，从数学角度分析, 信号即是某个物理量x的函数f(x), 信号所蕴含的信息需要通过此类函数予以揭示. 自然地可将f(x)投影到其所在空间中的一组基函数上, 由投影系数或加权系数来构成函数f(x)在变换域上的表示。在一定条件下这一过程是可逆的, 即由投影可以恢复f(x)。投影基函数选取的不同, 实质上是从不同角度对信号加以分析, 因此可以选取简单的基函数, 利用其所具备的性质来揭示函数f(x)的性质。上述投影过程被称为信号变换或信号表示。利用最简单的谐波(复正弦函数) 对信号进行投影或分解即为Fourier变换—由此不难看出, 信号表示是信号处理的基础。这正如处理欧氏空间的一般问题时, 需要利用一组基来表示空间中的任意点，即坐标与点的一对应关系。欧氏空间中基选取的不同, 将对空间中的操作(譬如线性变换) 产生重要影响。一定程度上, 合理的信号表示方法可以直接得到我们需要的信号中所蕴含的信息。

另外, 信号表示使得我们可以从其他角度审视信号(物理上, “其他角度”可理解为引入了新的物理量)。Fourier 变换引入了“频率” 这一物理量, 因而从频域角度分析信号, 使得我们可以更好地理解平稳信号, 进而得到信号中的关键信息。在频域上表示谐波, 使得谐波简单到只是一个δ函数。然而现实中却存在着许多非平稳的信号, 譬如语音、生物医学信号、机械振动等天然信号, 音乐、雷达信号、声呐信号等人工信号, 均为典型的非平稳信号。它们的特点是持续时间有限, 频率时变。显然对于频率随时间变化的信号, Fourier变换爱莫能助, 因此需要引入信号的联合表示等方法, 即同时从多个角度或是物理域来分析信号。

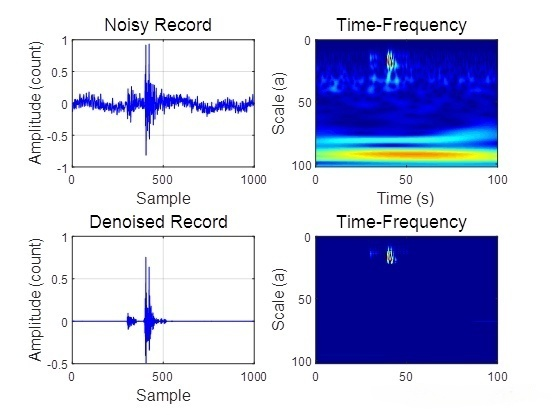
譬如下图所示,地面传感器获取的低空飞行的直升机的声音波形。从该波形上, 无从获得飞行高度、速度等信息, 频域中提供的信息也是很少。可见单独使用时域或者频域的方法都不能很好地处理该信号；但是直升机的直达声和反射声的时延差引起的干涉现象在时频面上弯度几乎成抛物线。由此可获得飞行高度、速度等信息. 概言之, 时频联合表示将时域或频域中不显然的信息, 变得显然。